What is Conic Section?- Definition, Overview, and Types

What is the Conic section?

When we talk about conic sections in mathematics, we’re referring to curves that show up when a plane slices through the surface of a cone. You’ve probably heard of the three classic types: hyperbola, parabola, and ellipse.

Technically, a circle also falls under the umbrella of ellipses though, in the past, people sometimes treated it as a separate fourth type.

These curves aren’t just a modern curiosity. Mathematicians in ancient Greece were already exploring their properties, with Apollonius of Perga putting together a landmark treatise on conic sections around 200 BC.

One of the fascinating things about conics in the Euclidean plane is how many unique ways there are to describe them. For instance, you can think of a non-circular conic as the set of all points that keep a fixed ratio (called eccentricity) between their distances from a specific point (the focus) and a given line (the directrix). The exact value of this eccentricity tells you which type of conic you’re dealing with.

If you take things into the realm of analytic geometry, conic sections become the solutions to quadratic equations in two variables, which you can even tidy up into matrix form. This algebraic approach opens the door to a whole new set of geometric insights.

Now, while hyperbolas, parabolas, and ellipses may look quite different at first glance, they actually have a lot in common beneath the surface.

And if you stretch the Euclidean plane a bit specifically, by adding in the so-called “line at infinity” to get what’s known as a projective plane the differences between them start to blur.

Suddenly, the two separate branches of a hyperbola meet up at infinity, making it one continuous curve, and the arms of a parabola wrap around to touch the line at infinity as well.

Take it one step further by letting your coordinates go complex instead of sticking to the real numbers, and you’ll find that all these curves are even more tightly connected than they first appear. It’s a neat demonstration of how geometry and algebra intertwine, especially when you’re willing to look beyond the ordinary plane.

Key Takeaway:

• Ellipse: An ellipse can be described as the set of all points (let’s call one of them P) that move in such a way that the ratio of their distance from a specific point, known as the focus (F), to their distance from a certain fixed line (the directrix) remains constant. Importantly, this constant is always less than one. In other words, as point P travels, it always maintains this unique ratio between the focus and the directrix, and that’s what gives the ellipse its distinctive, elongated shape.
• Parabola: A parabola is formed by all those points (imagine one, Q) that move so that their distance from a fixed point (the focus, F) is exactly equal to their distance from a fixed straight line (the directrix). Here, the ratio is always one—meaning, at every moment, Q is just as far from the focus as it is from the directrix. This special balance is what creates the symmetric, open curve we recognize as a parabola.
• Hyperbola: A hyperbola, on the other hand, is traced out by points (let’s refer to one as R) that move so the ratio of their distance from a fixed point (the focus, F) to their distance from a fixed line (the directrix) is a constant greater than one. So, as R moves, it’s always a bit farther from the focus compared to the directrix, according to this constant ratio—which is why the hyperbola has its characteristic twin-curve shape.

Definition

A conic section, often simply called a conic, comes from the intersection of a plane sometimes referred to as the cutting plane with the surface of a double cone. (Picture a cone that extends infinitely in both directions, forming two symmetrical parts, or “nappes.”)

Although it’s common to visualize a right circular cone to simplify explanations, that’s not a strict requirement; any double cone that has at least one circular cross-section will do the job.

Now, if you imagine the cutting plane passing exactly through the tip or vertex of the cone, the result isn’t one of the classic curves we associate with conics. Instead, you end up with something much simpler: the intersection forms a single point, a straight line, or two lines that cross each other.

These particular cases are called degenerate conics, and there’s some debate over whether they truly belong to the family of conic sections at all. For clarity, unless otherwise noted, “conic” here refers to the non-degenerate types.

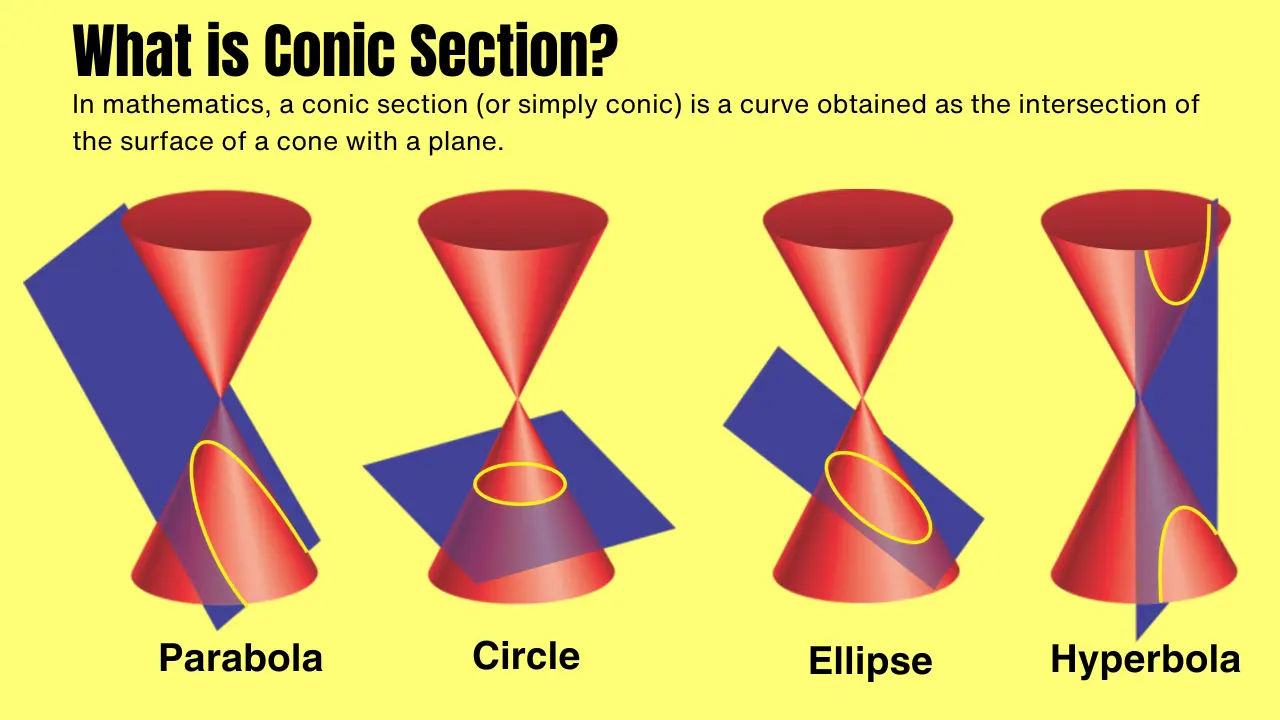
So, what are the main kinds of conics? There are three: ellipse, parabola, and hyperbola. (If you remember, a circle actually fits into this family as a special kind of ellipse, though in ancient mathematics, like the work of Apollonius, the circle was sometimes treated as its own separate type.)

Here’s how each arises:

• Ellipse: When the cutting plane slices through just one nappe, and it doesn’t go through the vertex, you get a closed, oval-shaped curve this is your ellipse.
• Circle: Take it a step further and make your cutting plane perfectly parallel to the base (the generating circle) of the cone. For a right circular cone, this means the plane is perpendicular to the axis of the cone. The resulting curve is a circle, the most symmetric ellipse.
• Parabola: If the plane is tilted so it’s parallel to exactly one of the cone’s straight sides (the generating lines), the curve you get doesn’t close up it keeps going forever in both directions. This is a parabola.
• Hyperbola: Lastly, if the cutting plane is even steeper, so that it slices through both nappes of the cone, you’ll see two separate, open curves appear. That’s the hyperbola.

In short, by simply changing the angle and position of a flat plane cutting through a cone, we end up with a rich family of curves each with its own distinct properties and importance in mathematics.

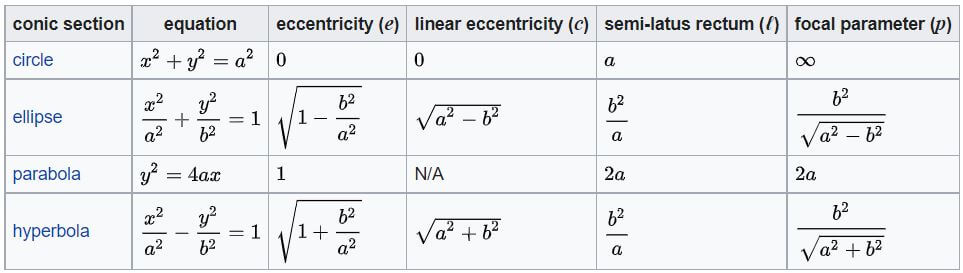
Equation, Eccentricity, Latus Rectum, Focal Parameter

Applications

Conic sections actually play a fascinating role in astronomy. If you imagine two massive bodies—like planets or stars—moving under the pull of gravity (the way Newton described), their orbits form conic sections, provided you treat their shared center of mass as not moving.

When these objects are gravitationally bound to each other, their paths are both ellipses. On the other hand, if they’re moving away from each other, you’ll see them tracing out paths that look like parabolas or hyperbolas instead.

But it’s not just about orbits! The unique reflective qualities of conic sections have found their way into the tools we build here on Earth. Take searchlights, for example.

Their reflectors are shaped like parabolic mirrors, with the light source (the bulb) sitting right at the focus point. This isn’t just a trick for lights—parabolic microphones use the same principle to pick up faint sounds from a distance.

Even giant telescopes get in on the action. The 4.2-meter Herschel telescope on La Palma, in the Canary Islands, uses a large parabolic mirror to gather and reflect incoming light toward a smaller, secondary mirror shaped like a hyperbola.

That secondary mirror then reflects the light again, bringing it to a focus just behind the main mirror. This clever setup is a testament to how deeply conic sections are woven into both our understanding of the universe and the technology we use to explore it.

FAQs