Elastic modulus, commonly known as Young’s modulus, represents the stiffness or resistance to elastic (non-permanent) deformation in the presence of a stress.
The elastic modulus of a material is an important property of interest to engineers and materials scientists in judging and measuring how a material can support dimensions and maintain its shape when the object is in service.
Please remember that the elastic modulus is really stiffness or resistance to STORE, that is done via stress (that is, forces per unit area), units being pascal (Pa) as used in SI units or pounds per square inch (psi).
The elastic modulus is derived through the elastic portion of the stress-strain curve, where the slope of the curve represents the elastic modulus value.
Values for elastic modulus vary considerably across materials depending on their atomic form and the nature of bonding. Stiffer materials will have a higher elastic modulus.
This article is an overview of the elastic modulus, how to measure it, what units it is expressed in and provides some examples of materials with some of the different values.

What Is Elastic Modulus?
The elastic modulus is defined as the ratio of stress to strain in the elastic (linear) portion of the scale of a material’s deformation, and is a measure of a material’s stiffness or the resistance of a material to elastic deformation.
Simply put, the elastic modulus is a measure of a material’s rigidity or stiffness, specific to a given stress and strain value. The modulus of elasticity, in terms of the stress-strain curve, is defined as the slope of the stress-strain curve in the elastic behaviour region where stress is linearly proportional to strain.
One of the most common specific types of elastic modulus is Young’s modulus (also known as the tensile modulus or modulus of elasticity in tension). Other types of elastic modulus include shear modulus and bulk modulus.
What Is the SI Unit of Elastic Modulus?
The elastic modulus is determined in pascals (Pa), which are also the SI units for stress. The elastic modulus is typically expressed in units of MPa or GPa to maintain the large magnitude of most typical values.
What Is an Example of Elastic Modulus?
Steel is commonly thought of, and used as a structural material, due its weight-bearing capabilities and ductility. The elastic modulus of steel typically falls within 200 to 210 GPa which depicts that it is very stiff and resists elastic deformation during applied stressful moments.
As a result; steel acts as a suitable candidate for structures that need strength and resiliency (such as beams in buildings or bridges) because steel demonstrates an elasticity during bending when loads are imposed. Steel can also yield or fail if stresses imposed are too great.
Steel also demonstrates factors of elasticity and moduli that are ideal for types of machine parts and tool application because the stiffness and resistance to bending are two advantageous factors.
Likewise, stiffness or elastic modulus of steel used in machines causes dimensional and motion stability and in turn helps produce precise parts with very little or no deflection or compliance under load. While elastic modulus can be high (like steel), this does not mean the material is brittle.
In fact, many forms of steel can remain stiff (high modulus) yet also portray ductility as a function alloying elements and heat treatment.
It is, therefore, highly advisable to reflect on the use of steel, its stresses, elastic/economic properties and the intended application in order to use this engineering material safely and effectively.
What Are the Elastic Modulus Values?
The elastic moduli for some common materials are listed in Table 1 below:
Table 1. Elastic Moduli of Some Common Materials
| Material | Modulus of Elasticity GPa | Modulus of Elasticity Mpsi |
|---|---|---|
| ABS | 1.0-2.7 | 0.15-0.39 |
| Acrylic | 2.8 – 3.3 | -0.41-0.48 |
| Aluminum | 69 | 10 |
| Copper | 110 | 16 |
| Glass | 70 | 10.2 |
| Magnesium | 45 | 6.5 |
| Nylon | 1.3-4.2 | 0.19-0.61 |
| Polypropylene | 1.1-1.6 | 0.16-0.23 |
| Steel | 200-210 | 29-30 |
| Titanium | 116 | 17 |
| Diamond | 700-1200 | 101.5-174.0 |
How Are the Values of Elastic Modulus Expressed?
Elastic modulus is generally expressed in unit of pressure (pascals (Pa) in SI, pounds per square inch (psi) in Imperial), and represents the stiffness (or resistance to elastic deformation) of the material when an applied stress is present.
There are multiple varieties of elastic modulus that differ based on the stress being applied. The most frequent type of elastic modulus is Young’s modulus, which identifies the ratio of stress to strain for stress that is applied perpendicular to the cross section area of the material.
The formula for Young’s modulus is:
- E=Young’s modulus, pressure units
- σ=uniaxial stress, or uniaxial force per unit surface, pressure units
- ε=strain, or proportional deformation (change in length divided by original length), dimensionless
Other forms of elastic modulus are the bulk modulus and the shear modulus. The bulk modulus measures the resistance to compression and the shear modulus measures the resistance to deformation in shear stress.
What Material Has the Highest Elastic Modulus?
Diamond has the highest elastic modulus, ranging from approximately 1050–1200 GPa and which is believed to be the “hardest material.” Compared to plastics and metals, this is much higher as compared to any type of plastic or metal.
The elastic modulus of plastics typically ranges roughly between 1.5 and 5 GPa depending on the type and formulation of the polymer.
Elastic moduli of metals are generally much higher than plastic. Elastic moduli of metals depend on the specific material and its composition, which can vary widely. Most metals, however, have elastic moduli that are between 50 and 400 GPa.
These ranges should be treated as general ranges for elastic modulus and it should be noted that the elastic modulus of a given metal can be influenced by things like temperature, strain rate, etc. but some metals might also have defects, impurities, etc.
What Does a Large Elastic Modulus Value Indicate?
A large elastic modulus indicates that a material is very stiff. It completely reflects that a high amount of stress generates only a small amount of elastic strain. Elastic modulus is an important design parameter when considering elastic deflections in structural or mechanical components.
What Does a Small Elastic Modulus Value Indicate?
A small elastic modulus suggests that it requires little force to induce a substantial amount of elastic strain. It is flexible, not stiff. It will easily deform elastically at only a very small applied tensile or compressive stress.
Rubber is an example of such a material with a very low elastic modulus approximately to 0.01 to 0.1 GPa, depending on the type and testing conditions.
What Is the Elastic Modulus Symbol?
The symbol for elastic modulus is E. This is Young’s modulus, which is the most common ‘flavor’ of elastic modulus. It is defined as the ratio of stress to strain in the linear (elastic) region of the stress-strain curve. Elastic Modulus (E) is measured in pascals (Pa) or pounds per square inch (psi).
How Is Elastic Modulus Determined?
The elastic modulus of a material is determined in its stress-strain curve by finding the slope of the linear (elastic) portion of this curve.
To determine the slope, a series of force applications as constant, increasing increments is applied to a material sample, and the stress and strain are measured. In this linear region, stress and strain are proportional, and their ratio gives the value for elastic modulus.
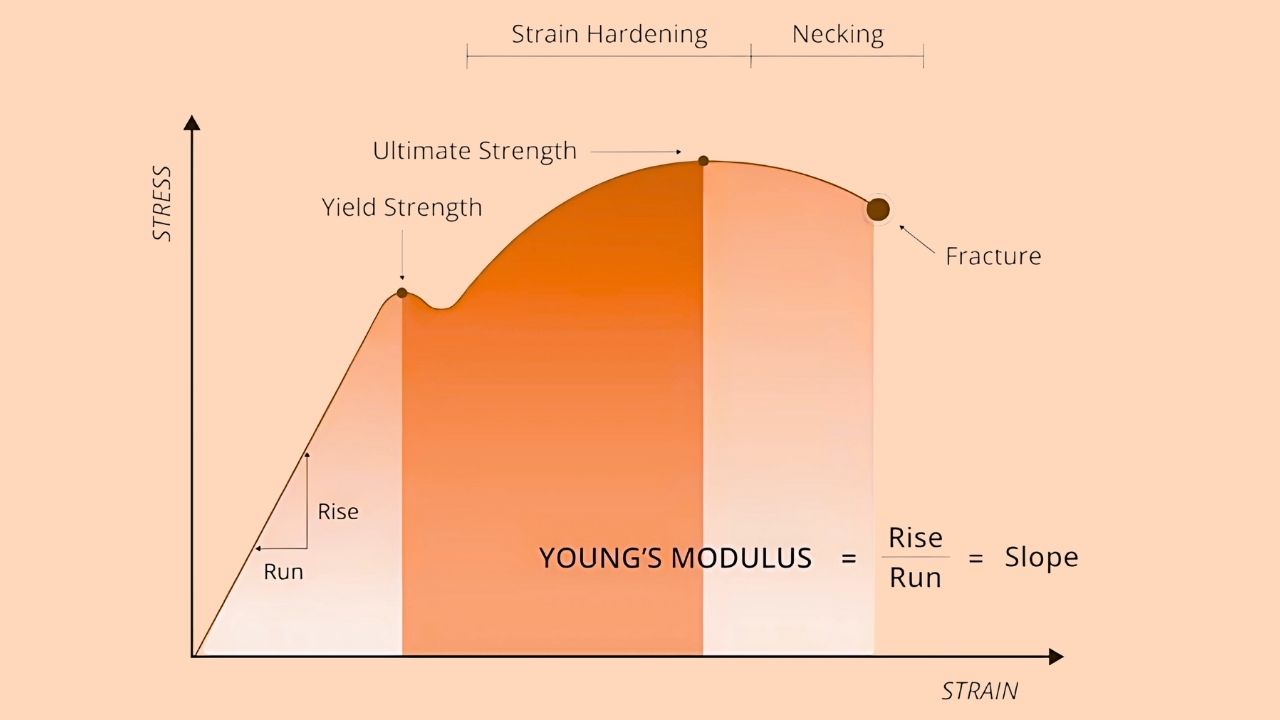
What Is the Elastic Modulus Equation?
The equation for elastic modulus (E) is:
Where σ is the stress, and ε is the strain in the elastic region of the material. For elastic modulus, the equation is simply the stress divided by strain.
What Is the Difference Between Elastic Modulus and Shear Modulus?
Elastic modulus (Young’s modulus) measures a material’s resistance to deformation under tensile or compressive stress. Shear modulus measures a material’s resistance to deformation under shear stress.
The primary difference between the two is the direction of the applied stress: elastic modulus measures resistance to normal (tensile or compressive) stress; shear modulus measures resistance to shear (parallel) stress.