Stress and strain stand at the heart of materials science and engineering, forming the basis for understanding how materials respond under various forces. Stress describes the amount of force exerted over a specific area of a material, while strain captures the resulting change in shape or deformation caused by that force.
Yet, the interplay between these two concepts is often more nuanced than it appears at first glance. The way a material behaves under stress and strain can vary widely, influenced by its composition, internal structure, and the nature of the load applied.
In the discussion that follows, I’ll walk you through the essential distinctions between stress and strain, highlighting their significance in engineering and design contexts. We’ll look at the various forms these concepts can take, examine the methods used to measure and interpret them, and consider how insights from stress and strain analysis help engineers anticipate the performance—and potential failure—of materials and structures.

What Is Stress?
Stress refers to the amount of force applied over a given area within a material. Understanding this concept is essential because it allows us to see how various materials respond when subjected to different kinds of forces.
Within any object, several forms of stress might arise such as compressive, tensile, shear, or torsional stress, to name a few. Each of these has its own way of influencing the material’s behavior, and we use different symbols to keep them straight. Most often, you’ll see stress represented by the Greek letter sigma (𝜎). To quantify stress, we rely on a straightforward mathematical formula, which is outlined below:
σ= F/A
Where:
- σ is stress, measured in N/m² or Pa
- F is the applied force, measured in Newtons (N)
- A is the cross-sectional area to which the force is applied, measured in m²
Among the various symbols used, 𝜎t stands for tensile stress, 𝜎c denotes compressive stress, and 𝜏 refers to shear stress.
How Stress in Materials Works
When a material, structure, or object is exposed to a force that causes deformation, internal stresses naturally arise. These stresses are essentially the material’s way of pushing back—an internal reaction to external demands.
Depending on how significant the force is, the object may deform in ways that are either entirely reversible (elastic deformation) or involve some lasting, permanent change (a mix of elastic and plastic deformation).
At the microscopic level, the atomic bonds inside the material are what resist these outside forces. They respond by generating a force that acts in opposition to whatever is being applied—a kind of internal counterbalance that keeps the object intact, at least up to a point.
Interestingly, even something as straightforward as pulling on a material (applying a tensile force along a single axis) doesn’t create stress in just that direction. Because the material stretches in one way and contracts in another, internal stresses actually emerge in more than one dimension.
To accurately capture what’s going on inside a loaded object, engineers and scientists use what’s known as a stress tensor. This mathematical tool reflects the complete, three-dimensional stress state, including how stresses in different directions interact with one another across the principal axes.
How Stress of Materials is Measured
Direct measurement of stress is not feasible; therefore, we rely on observing either the forces applied to a material or the deformations that result from those forces. In order to accurately measure deformation, it is essential to understand how applied forces referred to as stresses relate to the resulting deformations, or strains.
To assess stress indirectly, a range of experimental techniques and instruments are available. Common methods include the use of strain gauges, extensometers, piezoelectric sensors, load cells, ultrasonic measurements, x-ray diffraction, and photoelastic analysis. Each approach offers a way to capture the influence of applied forces by quantifying either the force itself or its effects on the material.
With the force determined, stress can be calculated using the well-established formula, σ = F/A, where F is the applied force and A is the cross-sectional area over which the force is distributed.
Stress analysis serves as a crucial aspect of understanding how different forces impact a given object. This analysis can be approached through experimental testing, computational modeling, analytical mathematics, or a thoughtful combination of these strategies.
The optimal method is chosen based on several factors, including the properties of the material, the specific type of stress in question, and the required precision of the results.
What Is Strain?
Strain describes how much a material changes shape when an external force is applied. In practical terms, it captures the extent to which a material stretches, compresses, or otherwise deforms when it experiences stress.
To quantify this, strain is calculated as the ratio between the change in a material’s length (or another dimension) and its original length.
Because both the numerator and denominator have the same units, strain itself has no units—it’s often shown as a simple number or as a percentage. The standard equation for strain, specifically when looking at changes in a specimen’s length, is shown below:
ε = L – Lo/ Lo
- Strain (ε) is the fractional or percentage change in length or another dimension.
- L is the length of the material after an external load is applied.
- L0 is its original length measured in the same units as “L”.
The terminology used to describe different types of strain is closely linked to the kind of stress a material experiences. For example, when a material is pulled and lengthened, we refer to the resulting deformation as tensile strain.
In contrast, compressive strain arises when a material is pressed together and shortened. Shear strain, on the other hand, occurs when the applied stress acts parallel to the material’s cross-section, causing layers to slide against one another.
When the change involves the material’s overall volume either expansion or contraction we call this volumetric strain. Finally, thermal strain describes the way a material’s dimensions adjust in response to changes in temperature, whether that means stretching, shrinking, or shifting in volume.
How Strain in Materials Works
When you apply an external force to a material, the material doesn’t just sit there it responds by deforming. This response, known as strain, essentially measures how much the material changes shape or size under that load.
Now, how a particular material behaves under stress isn’t just a matter of force alone. It actually hinges on several things: what the material is made of, its internal structure, and specifics about the force itself like its size, direction, and the way it’s applied. Broadly speaking, when subjected to stress, materials tend to deform in three primary ways:
- Plastic Deformation: When a material is pushed past its elastic limit by an applied stress, it begins to change shape in a way that cannot be reversed—even after the force is removed. This irreversible alteration is what we refer to as plastic deformation. A key point to note here is ductility: this describes just how much plastic deformation a material can experience before it ultimately fractures.
- Elastic Deformation: If a material is exposed to stress but manages to return to its original shape once the load is lifted, it’s undergoing elastic deformation. Essentially, the material can bend or stretch to a certain extent, but as long as it stays within this limit, there’s no permanent change.
- Fracture: A fracture takes place when the applied stress becomes greater than what the material can handle. At this stage, the material doesn’t just deform—it actually breaks apart or fails completely. In this context, a material’s strength is a measure of its ability to endure stress without either breaking or suffering from permanent deformation.
How Strain of Materials is Measured
There are several ways to measure strain, each with its own advantages. Among the most commonly used techniques are strain gauges and extensometers. Both of these require direct contact with the specimen and are sensitive to the direction of the applied force.
In addition to these traditional approaches, other options are available, such as digital image correlation (DIC), piezoelectric sensors, and acoustic emission sensors, each bringing its own strengths to strain measurement.
Key Differences of Stress and Strain
The key differences between stress and strain and listed in the chart below:
| Stress | Strain |
|---|---|
| The deforming force per unit area of the item is defined as stress. | Strain is defined as the amount of distortion experienced by the body in the direction of force application divided by the body’s original dimensions |
| The dimension is ML-1T-2 | It has no dimensions. |
| The unit for stress is Nm-2 | It has no unit. |
| The formula for stress is: σ = F/A | The formula for strain is: ϵ = δl/L |
| It is denoted by σ | It is denoted by ϵ |
| Longitudinal stress, shear stress, and volumetric stress are the different types of stress. | Longitudinal strain, shear strain, and volumetric strain are the three types of strain. |
| Stress can be applied to the object without producing strain. | Without stress, the strain cannot occur. |
Examples of Stress and Strain of Different Materials
Different materials exhibit different behavior when subjected to stress and strain. Here are some examples of stress and strain of different materials:
- Metals: When it comes to metals, their response to stress largely depends on their composition. Ductile varieties, such as stainless steel and numerous alloys, typically give way by bending and stretching rather than breaking right away. In contrast, brittle metals—think high-carbon steels—tend to snap with little warning and show hardly any noticeable stretching beforehand. Low-carbon steel occupies something of a middle ground: it will flex when loaded, but once it hits its yield point, it starts to harden as it strains. This change means it loses some of its original ductility and takes on more brittle characteristics, which in certain scenarios, can actually make it more vulnerable to sudden failure.
- Polymers: Polymers don’t fit neatly into one category; their stress-strain behavior is surprisingly varied.
The red curve illustrates the behavior of a brittle polymer, which breaks immediately after undergoing elastic deformation, without showing any signs of plasticity. In contrast, the blue curve shows how a plastic polymer responds, featuring both a yield point and a maximum stress level before failure.
As the material is stretched further, it eventually fractures. The stress measured at the point of fracture is referred to as the tensile strength. Elastomers, represented by the green curve, stand apart as a class of polymers known for their exceptional rubber-like elasticity. They can return to their original form after deformation, provided they are not stretched beyond their breaking point.
Even though some polymers can produce stress-strain curves that superficially resemble those of metals, their underlying mechanical properties are fundamentally different from both metals and ceramics.
To illustrate, a polymer with high elasticity may elongate up to ten times its original length before breaking, whereas a metal, in the elastic region, will typically extend only about ten percent, and may double its length if plastically deformed before it finally fractures.
Additionally, it’s important to note that the highest elastic modulus values observed in polymers are significantly lower than those found in either metals or ceramics.
How Stress and Strain Relate to Each Other
Stress and strain are fundamentally linked: whenever a material experiences stress, it responds with strain. The key to understanding this connection lies in Young’s modulus, a parameter that quantifies how the two relate.
Another important perspective comes from the concept of the elastic modulus, which essentially captures a material’s stiffness. In other words, it tells us how much a material will stretch or compress when subjected to a certain amount of stress.
This relationship is formally expressed through Hooke’s law. According to this principle, as long as a material remains within its elastic range, the amount of stress applied is directly proportional to the strain produced. Once a material surpasses its elastic limit, however, this straightforward relationship no longer applies. In mathematical terms, Hooke’s law is often written as:
σ = Eε
Where:
- σ is stress
- E is the elastic modulus
- ε is strain
It is worth emphasizing that Hooke’s law describes the behavior of materials only within their elastic range. In this state, materials will return to their original shape and size once the applied stress is removed. However, if a material is pushed past its elastic limit, it begins to deform plastically, and at that point, Hooke’s law no longer holds true.
The Stress-Strain Curve
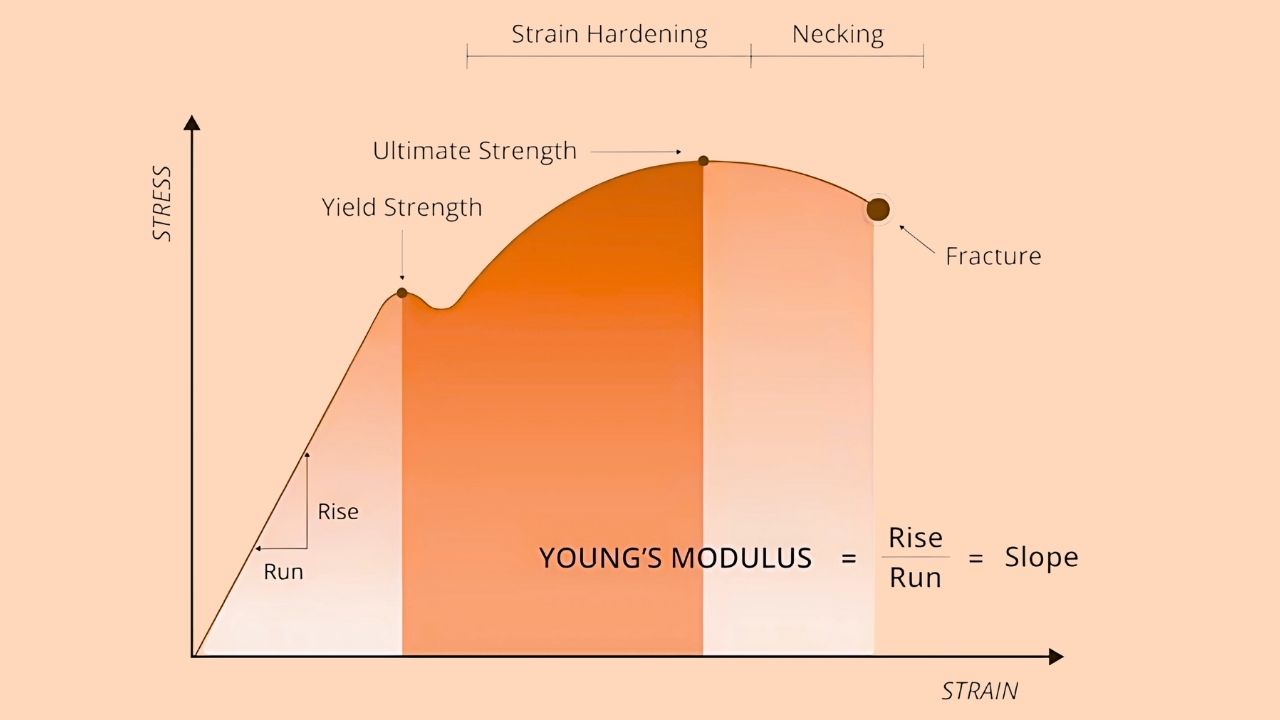
A stress-strain curve offers a visual account of how a material responds when exposed to gradually increasing stress. By steadily loading a material sample and observing the resulting strain, we capture the curve that characterizes the material’s behavior under stress.
These diagrams play a key role in assessing how a material behaves all the way from initial loading up to the point of failure. Interestingly, each material tells its own story through its unique stress-strain pattern details that engineers rely on to gauge important mechanical properties like strength, elasticity, yield point, resilience, ductility, toughness, and strain energy.
This insight proves essential when it comes to designing components or processes such as rolling, extrusion, or bending, as it enables us to estimate the necessary force to cause plastic deformation.
Typically, the stress-strain curve is divided into two main regions: the elastic region and the plastic region. In the elastic region, a material temporarily changes shape in response to applied stress, but as soon as the stress is lifted, it snaps right back to its original form.
Here, the relationship between stress and strain remains linear, and the slope—often called Young’s modulus or elastic modulus—reflects the material’s stiffness.
Once the material enters the plastic region, the story changes: any further deformation becomes permanent, so the material won’t recover its original shape even after the stress is removed.
The connection between stress and strain in this region is nonlinear, shaped by properties such as the material’s yield strength, ultimate strength, and ductility.